Bits for Beginners

What is equivalence?

Two positions or moves are equivalent if they can be considered the same as far as the overall game is concerned. There are three broad types of equivalence, listed here in order of increasing complexity:

1. Primary tile: two moves are equivalent if they have an identical effect on the pattern of tiles after the move.
2. Symmetry: two positions are equivalent if they are mirror images or rotations of each other.
3. Position equivalence: two different positions are equivalent if playing equivalent moves results in positions which are also equivalent.

These are described in more detail in the main article.

Why is equivalence important?

It reduces the number of moves that we need to consider. This is important because there are many more moves that can be played in a position than most players realise. In a straight-forward position 6x6 tiles, there typically about 60 moves that can be made.

The position equivalence principles enable us to understand how apparently different looking positions actually behave the same. Equivalence may be applied not only to the complete playing area, but also to localised regions. This can help us to understand better how various threats work, and therefore enable us to improve our play.

Trax Tips

I will describe five "equivalence principles" that are useful when analysing any Trax position. The first three aren't really principles, but are techniques that help to reduce the number of moves to consider playing under certain situations, and the last two make it easier to visualise what a position contains.

1. Primary Tile Equivalence

Primary tile equivalence occurs when two different primary tiles (the first tile played in a move) result in identical positions. For example, in the position here, it doesn't matter if @1/ or @2\ is used since both moves are the same. Playing one tile forces the other.

A similar situation occurs in hollows where there may be several equivalent moves. For example in this position B2/ = B1\ = C2\. Any one of these moves forces the others. In caves where moves may be even more constrained, it is possible to have four or more equivalent moves.

Primary tile equivalence is a direct result of forced plays. By recognising that playing different primary tiles can give the same position under some circumstances reduces the number of primary tiles that need to be considered.

The obvious question is when does primary tile equivalence occur? It occurs whenever paths of the same colour entering adjacent spaces are linked. Turning either path towards the other has the same effect. It also common next to and in hollows because the space in the hollow has both black and white paths entering it.

Symmetry can also be used to reduce the number of moves to consider. There are two types of symmetry - same colour symmetry and opposite colour symmetry. Both types are common at the start of games. Once a position gets larger, symmetrical positions become rarer.

2. Same colour symmetry

A position is same colour symmetrical when it matches itself when reflected or when rotated by 180°. Examples of same colour symmetry are shown here:
In positions which are same colour symmetric, we only need to consider half the number of moves. For example in the first position, if we look at what can be played at @1, we don't need to consider the equivalent moves at D1.

A position with same colour symmetry will always be symmetrical in both colours. This means that if we make a symmetrical position, we only need to consider half the number of responses. It also means that if we make a mistake, our opponent is twice as likely to find the winning move!

3. Opposite colour symmetry

A position is opposite colour symmetrical when it matches itself with colours reversed when rotated or reflected. Examples are:
Such positions are equivalent for each colour. Therefore a good move for one player will have a corresponding good move for the other player. The person with the next move usually has an advantage in positions with opposite colour symmetry, because they have first go at using the position. You should take care before creating such a position, especially if it looks good for you!

It is possible to have positions with both types of symmetry as the next two examples illustrate:

4. Path equivalence

Path equivalence is a little more complicated than primary tile equivalence and symmetry. Consider the following two positions. Although they look quite different, they are actually equivalent as far as playing the next move is concerned.
It doesn't matter how convoluted a path is, it is where the ends come out that is important. If you look carefully, you will notice that each path comes out in exactly the same place in each of the positions, even though most of the paths take a different route from one end to the other. As far as playing goes, they can be considered equivalent.

This principle may be used to simplify the position as an aid to understanding it and recognising any threats. If we replace each of the paths in the above position with a simple path going between each of the ends we get something like the position here. Note that although this is not actually a Trax position, it contains all the useful information in an equivalent form. Notice how much easier it is to see what is going on. Since this is equivalent, why not use this rather than either of the original positions. Obviously, when we are playing across the table, we cannot physically reconstruct the position as shown. However we can do it mentally. Reducing a convoluted path to its simple equivalent in our mind may help us to recognise a threat that we may otherwise miss.

5. Hollow equivalence

Path equivalence can be extended one step further. Consider the two positions shown below. They are equivalent according to our path equivalence principle apart from in the hollow at the base of the L in the top right corner. The edges from which the black and white paths enter the hollow have been swapped. When we activate the Ls with D1/, the attacks formed are completely equivalent. Since the two positions are equivalent after playing equivalent moves to each position, the positions must have been equivalent before the move was played. In other words when two paths enter a hollow, the position is equivalent even if the direction that the paths come into are swapped around.

Using this principle can help us to recognise variations of threats. The standard L and short L just shown are just one example of variations of threats being equivalent. Whenever we see a hollow, we can mentally swap the paths around, and check if the corresponding equivalent position is one that we recognise.

Summary

The equivalence principles provide powerful tools that enable us to simplify the analysis of a position. Primary tile equivalence allows us to reduce the number of moves we need to consider in places like caves and hollows. We only need to look at half the number of moves in a position with same colour symmetry. In a position with opposite colour symmetry, any good moves for one player will also be present for the other player. Path equivalence allows us to reduce a position to its basic components, and can simplify a position considerably. This can help us to recognise threats more easily. Path equivalence may be extended into hollows, allowing us to recognise threat variations as being equivalent. Finally, path equivalence may be combined with symmetry, so that positions which may not appear to be symmetrical are actually symmetrical in an equivalent sense.

Extras for Experts

The path equivalence principle has significant implications in terms of threat recognition. Since the route the paths take between the ends does not matter, we only need to look at the ends and how they are connected. This means that in terms of describing threats, we can get away from the tiles all together, and represent the threat in an abstract form. I will illustrate this by way of example. Consider the L threat here:
The position on the left shows the threat using Trax tiles. We then use the path equivalence principle to reduce the threat to its simplest form. Note that we are no longer using tiles, but we are still representing the paths taken. We can do away with the physical layout altogether if we have some way of labelling changes in orientation. Here I have used + to indicate an outside or convex bend, and - to indicate an inside or concave bend. If we just keep their labels and their connectivity information, we have:
We can use subscripts instead of ties to indicate the ends that are connected:
This represents all of the essential information in our original L in a much more compact form. This notation also allows us to generalise the threat more easily, and look at a whole family of threats. For this we will look at the individual components of the threat.

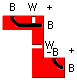
Starting with the corner at the top of the L, this may be any corner that allows us to make an attack. That means the top corner may consist of B₁ [W] + [W] B₁, where the items in square brackets are optional. We could also use a flat corner at the top: B₁ W W [W] B₁. We can combine the two together as
where the curly brackets indicate that one of the items contained must
be selected.

For the bottom corner, we may have either a simple corner (B₂ + B₂), a long corner (B₂ + W B₂), or a short flat corner (B₂ W W B₂). This may be represented as:
Combining these together gives:
We can now use the hollow equivalence principle to generalise this in 2 further ways. First, the W - B₂ in the hollow could also be B₂ - W, giving a so-called short L rather than a standard L. Also the B₁ at the start and B₂ at the end may be in a hollow. In this case, we can swap the paths in the hollow around giving B₁ [- W] and [W -] B₂ respectively.

These make the representation of the standard L (in all of its generalisations) to be: